自信息
量化事件的信息量 \(I(X=x)=-log p(X=x)\) # 信息熵 对概率分布不确定性总量的量化(信息量的期望):
\(H(X) = E_{X}(I(X))=-\sum_{x\in X}p(X=x)logp(X=x)\)
条件熵
表示在已知随机变量 X 的条件下,随机变量 Y 的不确定性(熵)
\(H(Y|X)=\sum_{x\in X} P(X=x)H(Y|X=x)\)
信息增益
某个随机变量的信息熵-该变量的条件熵
\(IG(Y,X)=H(Y)-H(Y|X)\)
该方法的决策树 ID3 所选择的特征会偏好于属性值较多的特征
Gini 系数
将熵定义中的 \(-log(p(x))\) 替换成 \(1-p(x)\)
\(Gini(X)= \sum_{x\in X}p(X=x) (1-p(X=x))=1-\sum_{x\in X}p(X=x)\) 基于 Gini 系数的决策树同样具有偏好于属性值较多的特征的问题
信息增益率
\(GainRatio(Y,X) = IG(Y,X)/H(X)\)
直接采样该方法的决策树又会偏好属性取值较少的特征。因此,决策树 C4.5 先通过一遍筛选,先把信息增益低于平均水平的属性剔除掉,之后从剩下的属性中选择信息增益率最高的.
交叉熵
P 为某样本真实分布,Q 为该样本的估计分布,如果用估计分布 Q 来表示真实分布 P 的平均编码长度就是交叉熵,当我们对分布估计不准确时,总会引入额外的不必要信息期望(可以理解为引入了额外的偏差)
\(H(P, Q)=-\sum_{x}P(x)log(Q(x))\)
相对熵(KL散度)
用估计的概率分布来表示真实分布多使用的信息量。估计分布表示真实分布所用的平均编码长度-用真实分布编码的平均长度=相对熵
\(D(P|Q)=KL(P,Q)=H(P,Q)-H(P)\\=-\sum_{x}P(x)log(Q(x))+sum_{x}P(x)logP(x)\\=\sum_{x}P(x)log\frac{P(x)}{Q(x)}\)
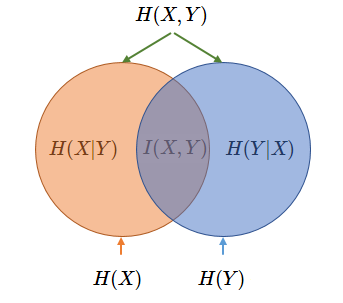
互信息
两个随机变量的联合分布 (P) 与它们的独立分布的乘积 (Q) 之间的相对熵, 两事件的互信息为各自事件单独发生所代表的信息量之和减去两事件同时发生所代表的信息量之后剩余的信息量,这表明了两事件单独发生给出的信息量之和是有重复的,互信息度量了这种重复的信息量大小
\(I(X;Y)=\sum_{x\in X}\sum_{y \in Y} p(x,y)\frac{p(x,y)}{p(x)p(y)}\)
困惑度
给定语言L的样本 \(l_1^n=l_1,l_2,...,l_n\),模型对数据的困惑度为
\(2^{H(L,q)}\approx 2^{-\frac{1}{n}log q(l_1^n)}={[q(l_1^n)]}^{-\frac{1}{n}}\)
参考 (References)
- https://baike.baidu.com/item/%E7%9B%B8%E5%AF%B9%E7%86%B5/4233536?fr=aladdin
- https://baike.baidu.com/item/%E4%BA%92%E4%BF%A1%E6%81%AF/7423853?fr=aladdin
- https://www.zhihu.com/question/41252833
- https://zhuanlan.zhihu.com/p/136100996