EM 基本思想
已知观察数据,未知隐含数据和模型参数。在E步,我们所做的事情是固定模型参数的值,优化隐含数据的分布(猜想隐变量的数据),而在M步,我们所做的事情是固定隐含数据分布,优化模型参数的值(基于观测数据和猜测的隐变量数据最大化对数似然函数)
这个算法与 MLE(maximum likelihood estimation)的差别是:MLE 针对无隐变量的模型,先收集所有变量的观测数据,然后根据完整的观测数据去估计参数;EM 针对含隐变量的模型,先根据可观测变量的数据猜测隐变量的数据,然后根据隐变量数据和观测数据来估计参数 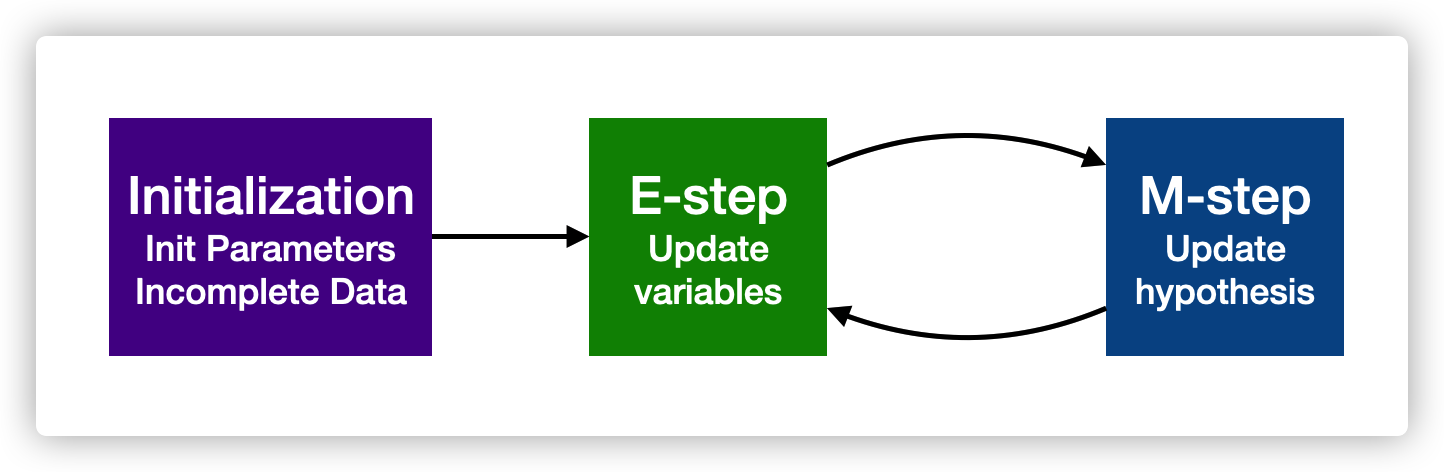
EM 推导
Jensen’s inequality
如果函数 \(g(x)\) 是凸函数,那么有 \(g(E(x))\geq E(g(x))\)
证明如下,过点 \((x, g(E(x)))\) 所一条切线,假设切线公式为 \(L(x)=a+bx\) 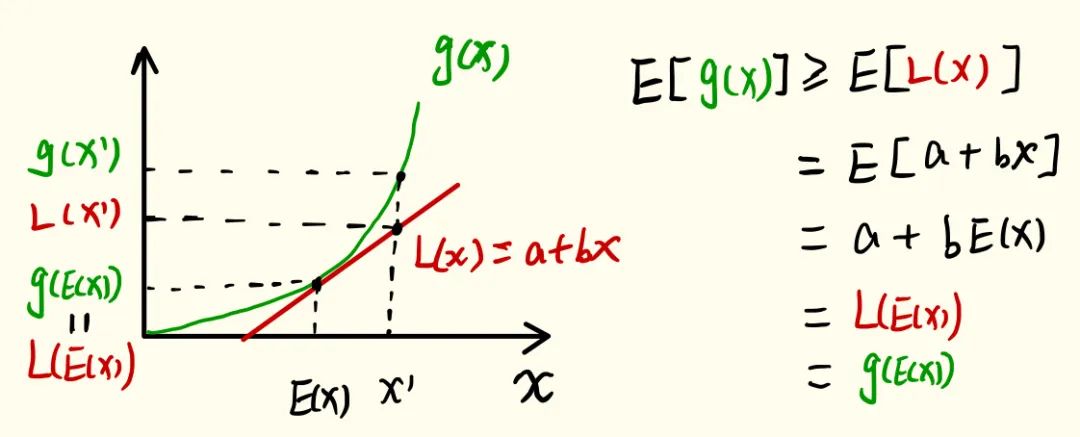
EM 算法
整体思想
假设有 \(n\) 个独立同分布的数据 \({x^{1}, x^{(2)},...,x^{(n)}}\),我们要估计一个包含隐变量 \(z\) 和变量 \(x\) 的模型的参数,改模型表示为 \(p(x,z;\theta)\),
那么,关于变量 \(x\) 的概率密度为 \(p(x;\theta)=\sum_{z} p(x,z;\theta)\)
模型的训练目标为极大对数似然函数 \(l(\theta)=log(\sum_{i=1}^{n}p(x^{(i)};\theta))=\sum_{i=1}^{n}\sum_{z^{(i)}}p(x^{(i)}, z^{(i)};\theta)\)。由于 \(z\) 是隐变量,数据无法观测,优化这个目标是困难的
EM 算法,通过构造 \(l(\theta)\) 的下界函数,通过在 E 步根据参数和部分观测数据计算下界函数,在 M 步最大化下界函数来实现对参数 \(\theta\) 的逐步优化
下界函数 ELBO 推导
先考虑对一个数据样例 \(x\) 的优化过程,即针对目标 \(log(p(x;\theta))=log(\sum_{z} p(x,z;\theta))\),令分布 \(Q(z)\) 为隐变量 \(z\) 的一个分布,\(\sum_{z}Q(z)=1, Q(z)\geq 0\),此时重写目标
\(log(p(x;\theta))=log(\sum_{z} p(x,z;\theta))=log\sum_{z}Q(z)\frac{p(x,z;\theta)}{Q(z)} \geq \sum_{z}Q(z)log\frac{p(x,z;\theta)}{Q(z)}\)
上面不等式根据 Jensen 不等式可推导,因为 \(log(\frac{p(x,z;\theta)}{Q(z)})\) 是一个关于 \(z\) 的凸函数
Q 函数的确定
对于任意一个 \(Q(z)\) 上面的不等式都成立,但是我们希望找到的下界函数跟目标函数足够接近(也就是令不等式的等式成立),此时必须满足条件 \(\frac{p(x,z;\theta)}{Q(z)}=c\),这意味着 \(Q(z)\sim p(x,z;\theta)\),而 \(\sum_z Q(z)=1\)(归一化概率分布),因此我们可以计算出 \(Q(z)\) 为
\(Q(z)=\frac{p(x,z;\theta)}{\sum_{z} p(x,z;\theta)}=\frac{p(x,z;\theta)}{p(x;\theta)}=p(z|x;\theta)\)
这样我们就唯一确定了 \(Q(z)\) 函数为 \(z\) 的给定观测数据 \(x\) 和参数 \(\theta\) 的后验概率,即给定了观测数据和参数,就可以猜测出 \(z\) 的概率分布(隐数据),基于此就计算出了一个新的 ELBO
EM 算法
在此重写我们的目标函数和下界函数的关系
\(l(\theta)=\sum_{i}log(p(x_i;\theta))\geq \sum_{i}ELBO(x^{(i)};Q_i(z^{(i)}),\theta)=\sum_{i}\sum_{z^{(i)}} Q_i(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\),对于任意 \(Q_i,i=1,2,...,n\) 必须满足 \(Q_i(z^{(i)})=p(z^{(i)}|x^{(i)};\theta)\)
Initialization
随机初始化 \(\theta\)
E-step
对于每一个 \(i\),令
\(Q_i(z^{(i)}):=p(z^{(i)}|x^{(i)};\theta)\)
M-step
\(\theta:=\underset{\theta}{argmax}\sum_{i}^{n} ELBO(x^{(i)};Q_i,\theta) =\underset{\theta}{argmax}\sum_{i}^{n}\sum_{z^{(i)}}Q_i(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\)
收敛性证明
\(l(\theta^{(t+1)})\geq \sum_{i=1}^{n} ELBO(x^{(i)},Q_i^{(t)},\theta^{(t+1)}) \geq \sum_{i=1}^{n} ELBO(x^{(i)},Q_i^{(t)},\theta^{(t)}) =l(\theta^{(t)})\)
其中 \(\theta^{(t+1)}\) 是通过 \(\underset{\theta}{argmax} \sum_{i=1}^n ELBO(x^{(i)};Q_i^{(t)},\theta)\) 求出来的最优参数
应用
K-means 算法
K-means 算法开始给定随机的聚类簇的中心(簇的中心就是隐变量),根据聚类簇的中心划分数据。在 E 步中估计 K 个簇的中心位置。然后计算得到每个样本最近的质心,并把样本聚类到最近的这个质心,这个就是 M 步