空间几何基础
点到平面距离公式
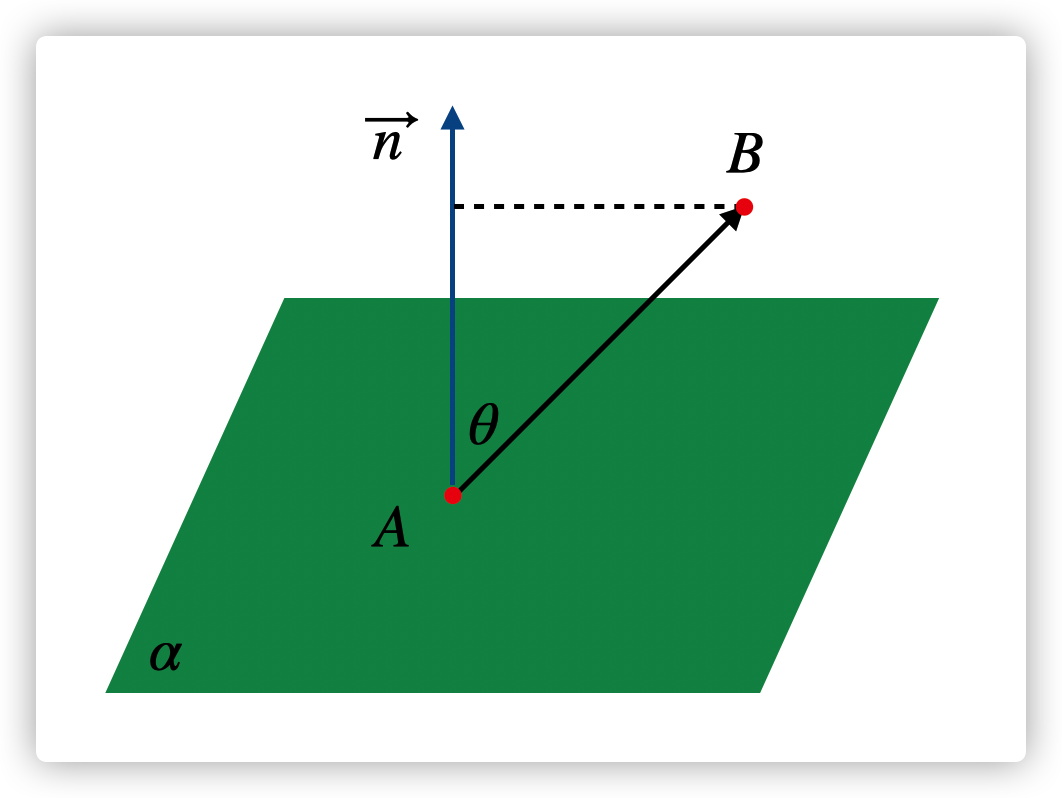
如图，有一个平面 $: \(ax+by+cz+d=0\)，它的法向量 \(\vec n=(a,b,c)\)（平面内任意一个向量与 \(\vec n\) 的点积为 0），求平面外一点 \(B=(x_1,y_1,z_1)\) 到平面 \(\alpha\) 的距离 取平面内任意一点 \(A=(x_0,y_0,z_0)\)，则向量 \(\overrightarrow{AB}=(x_1-x_0,y_1-y_0,z_1-z_0)\) ，点 \(B\) 到平面 \(\alpha\) 的距离等于 \(|\overrightarrow{AB}|cos\theta\)，而 \(cos\theta=\frac{\vec n \cdot \overrightarrow{AB}}{|\vec n|| \overrightarrow{AB}|}\)，
因此点 \(B\) 到平面的距离 \(h=\overrightarrow{AB}\cdot \frac{\vec n}{|\vec n|}=\left|(x_1-x_0,y_1-y_0,z_1-z_0)\cdot \frac{(a,b,c)}{\sqrt{a^2+b^2+c^2}} \right|=\frac{|a(x_1-x_0)+b(y_1-y_0)+c(z_1-z_0))|}{\sqrt{a^2+b^2+c^2}}\)，
又 \(ax_0+by_0+cz_0+d=0\)，所以最终点 \(B\) 到平面的距离为 \(h=\frac{|ax_1+by_1+cz_1+d|}{\sqrt{a^2+b^2+c^2}}\),
推广到 n 维空间中点 \(A=(x_1,x_2,...,x_n)\)，超平面 \(\pi\): \(a_1y_1+a_2y_2+...+a_ny_n+d=0\)，则点 \(A\) 到平面 \(\pi\) 的距离为 \(\frac{|a_1x_1+a_2x_2+...+a_nx_n+d|}{\sqrt{ {a_1}^2+{a_2}^{2}+...+{a_n}^2}}\)
两个平面之间的距离
已知两个超平面 \({\pi}_1\): \(a_1x_1+a_2x_2+...+a_nx_n+d_1=0\) 和超平面 ${}_2: \(a_1y_1+a_2y_2+...+a_ny_n+d_2=0\)。 取 \({\pi}_1\) 中任意一点 \(P(x_1,x_2,...,x_n)\)，则 \(P\) 到 \(\pi_2\) 的距离为 \(h=\frac{|a_1x_1+a_2x_2+...+a_nx_n+d_2|}{\sqrt{ {a_1}^2+{a_2}^2+...+{a_n}^2 }}\)。由于 \(P\) 在平面 \(\pi_1\) 上，所以有 \(a_1x_1+a_2x_2+...+a_nx_n+d_1=0\)，最后 \(h=\frac{|d_2-d_1|}{\sqrt{ {a_1}^2+{a_2}^2+...+{a_n}^2}}\)
SVM 间隔
函数间隔
令 \(w^Tx+b=0\) 为我们的划分超平面，对于任何一个数据点 \(x\)，它的标签为 \(y\in [-1,1]\)，我们规定，当 \(w^Tx+b>0\)，\(x\) 被划分为正例，当 \(w^Tx+b<0\)，\(x\) 被划分为反例。定义函数间隔为
\(\gamma(x) = y(w^Tx+b)=yf(x)\)
当 \(\gamma > 0\)，那么说明数据点 \(x\) 被正确分类
那么 SVM 训练的目标为 \(\hat \gamma = min\ \gamma(x_i), i = 1,2,...,n\)
几何间隔
由于函数间隔 \(\hat\gamma\) 的值会随着参数 \(w\) 和 \(b\) 的缩放（超平面不变）而变化，比如 \(w\) 和 \(b\) 变成 \(2w\) 和 \(2b\)，\(f(x)\) 会变成 \(2f(x)\)，如果按照最小化函数间隔，永远求不出个最优的参数 \(w\) 和 \(b\)。为此将目标给为最小化几何间隔
\(\tilde \gamma=\frac{y(w^Tx+b)}{||w||}=\frac{yf(x)}{||w||}=\frac{\gamma(x)}{||w||}\)
其中 \(\frac{f(x)}{||w||}\) 其实就是点 \(x\) 到超平面 \(w^Tx+b=0\) 的几何距离
最大间隔分类器
对于我们的分类器，希望最大化 \(max\ \tilde{\gamma}\)，并且对所有的数据点要满足 \(y_i(w^Tx_i)+b=\gamma(x_i)\geq \hat \gamma, i=1,2,...,n\)。
这里我们可以取 \(\hat \gamma=1\)（这个值可以随意取一个大于 0 的数，参数 \(b\) 可以在训练过程中调整），如此 SVM 的优化目标为
\(max\frac{1}{||w||},\ s.t.,\ y_i(w^Tx_i+b)\geq 1,i=1,2,...,n\)
这个问题的优化目标就如下图所示
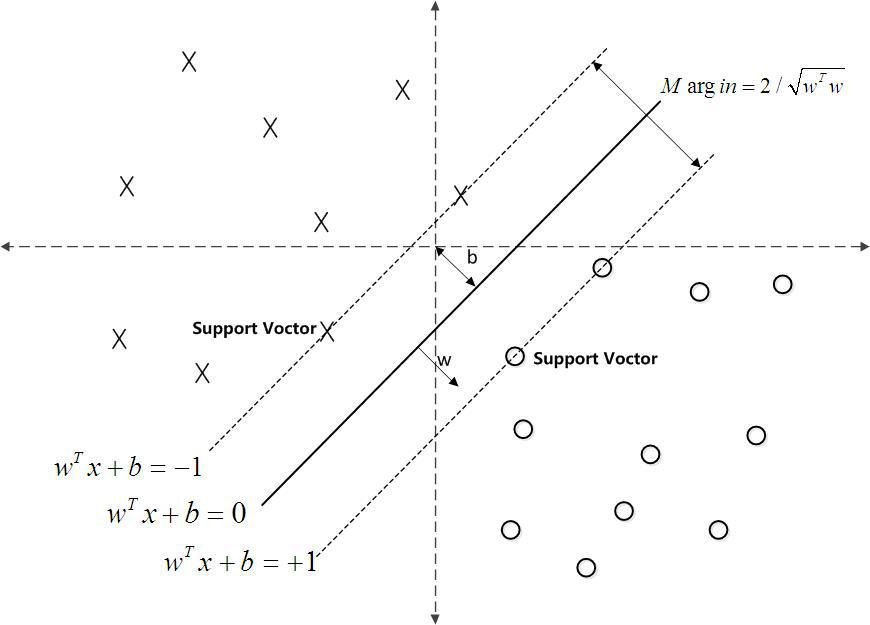
深入推导
线性可分问题
Max 问题变为 Min 问题
\(min\frac{1}{2}||w||^2,\ s.t.,\ y_i(w^Tx_i+b)\geq 1,i=1,2,...,n\)
对偶问题转化
上面的问题是一个凸二次规划问题，可以直接用现成优化方法。还可以用朗格朗日对偶性，将原问题变化成它的对偶问题来求解。这样做的好处：（1）对偶问题更容易求解；（2）方便引入核函数
定义拉格朗日函数
\(L(w,b,\alpha)=\frac{1}{2}||w||^2-\sum_{i=1}^n \alpha_i(y_i(w^Tx_i+b)-1)\)
现在来看，我们的目标为 \(\underset{w,b}{min}\ \underset{\alpha_i\geq 0}{max}\ L(w,b,\alpha)=p^*\)
其中 \(p^*\) 为问题的最优值。容易验证，如果有那个条件 \(y_i(w^Tx_i+b)<1\) 不满足，那么里面的 \(max\) 问题就会趋向 \(\infty\)，只有当所有的条件都满足时，才能求出外面的 \(min\) 问题，最小值为 \(\frac{1}{2}||w||^2\)
此时对换 \(min\) 和 \(max\) 就得到了原问题的对偶问题
\(\underset{\alpha_i\geq 0}{max}\ \underset{w,b}{min}\ L(w,b,\alpha)=d^*\)
其中 \(d^*\) 为问题的最优值，并且满足 \(d^*\leq p^*\)。由这个对偶问题，从而实现先对 \(w\) 和 \(b\) 极小化，然后对 \(\alpha_i\) 极大化
注： 只有原问题能满足 KTT 条件才能转化为它的对偶问题来求解。 KTT 条件定义如下：
对于一个凸函数 \(f(x)\)，求解 \(min\ f(x)\)
\(s.t. h_j(x)=0,j=1,...,p;\ g_k(x)\leq 0,k=1,...,q\)
KTT 条件如下： 1. \(h_j(x)=0,j=1,...,p;\ g_k(x)\leq 0,k=1,...,q\) 2. \(\bigtriangledown f(x)+\sum_{j=1}^p \lambda_j\bigtriangledown h_j(x) + \sum_{k=1}^q \mu_k\bigtriangledown g_k(x) = 0, \lambda_j\neq 0,\mu_k\geq 0, \mu_kg_k(x)=0\)
问题求解 1. 固定 \(\alpha_i\)，最小化 \(w\) 和 \(b\)
$\frac{\partial L}{\partial w}=0 \Rightarrow w=\sum_{i=1}^n \alpha_i y_i x_i$
$\frac{\partial L}{\partial b}=0 \Rightarrow b=\sum_{i=1}^n \alpha_i y_i=0$
代入 $L(w,b,\alpha)=\frac{1}{2}||w||^2-\sum_{i=1}^n \alpha_i(y_i(w^Tx_i+b)-1)$ 得到
$L(w,b,\alpha)$
$=\frac{1}{2}\sum_{i,j=1}^n \alpha_i\alpha_jy_iy_jx_i^Tx_j-\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j-b\sum_{i=1}^n \alpha_i y_i+\sum_{i=1}^n \alpha_i$
$=\sum_{i=1}^n \alpha_i-\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j$代入上一步求解的最优 \(w^*\) 和 \(b^*\)，然后对 \(\alpha\) 最大化
由上一步求出了新的朗格朗日函数不包含 \(w\) 和 \(b\)，得到：
\(\underset{\alpha}{max}\sum_{i=1}^n \alpha_i-\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_i^Tx_j\)
\(s.t.,\ \alpha_i\geq 0,i=1,...,n\)
\(\sum_{i=1}^n \alpha_i y_i=0\)
求得 \(L(w,b,\alpha)\) 关于 \(w\) 和 \(b\) 最小化，以及对 \(\alpha\) 的极大化之后，最后使用 SMO 算法求解对偶问题中的拉格朗日乘子 \(\alpha\)，由此可以求出 \(\alpha_i\)
根据 \(w=\sum_{i=1}^n \alpha_i y_i x_i\) 可求出 \(w\), 然后通过 \(b^*=y_j-\sum_{i=1}^n\alpha_i y_i(x_i^Tx_j),\alpha_j>0\) 求出 \(b\)。而分类函数 \(f(x)=w^Tx+b\)，其中 \(w=\sum_{i=1}^n \alpha_iy_ix_i\)，代入得到分类函数 \(f(x)=\sum_{i=1}^n \alpha_iy_i\langle x_i,x\rangle+b\)
线性不可分问题
由上面的分类函数可以看出，新的数据点 \(x^*\) 的分类，只需要计算它与训练数据点的内积即可（可用于推广 Kernel）。而 SVM 中的支持向量（supporting vectors）是对应 \(\alpha_i\neq 0\) 的训练数据点。
感性理解就是，\(x^*\) 分类其实只与分类超平面有关，而这个超平面只受支持向量的影响，所以其他的训练数据点不需要参与决策
理性理解，回到我们的拉格朗日乘式子，\(\underset{\alpha_i\geq 0}{max}\ \frac{1}{2}||w||^2-\sum_{i=1}^n \alpha_i(y_i(w^Tx_i+b)-1)\)
对于一个支持向量来说，\(y_i(w^Tx_i+b)-1=0\)，\(\alpha_i\) 可以不为 0；对于非支持向量的数据点来说\(y_i(w^Tx_i+b)-1>0\)， 为了求极大，必须满足 \(\alpha_i=0\)（\(\alpha_i\geq 0\)）
松弛变量使用
加入松弛变量是为了解决离群点的问题，因为当训练数据中存在函数间隔大于 1 时，采用一个松弛变量来实现对一些数据点的软间隔
由此，原目标函数：
\(max\ \frac{1}{2}||w||^2;\ y_i(w^Tx_i+b)\geq 1,i=1,...,n\)
就变成了新的目标函数：
\(max\ \frac{1}{2}||w||^2+C\sum_{i=1}^n \xi_i;\ y_i(w^Tx_i)-b\geq 1- \xi_i, \xi_i\geq 0,i=1,...,n\)
其中 \(C>0\) 用于平衡对两个目标：（1）最大化几何间隔；（2）使误分点尽量少。当 \(C\) 很大时，对误分类的惩罚大（着重考虑减少误分点）；相反，就更重视最大化几何间隔
用拉格朗日乘数法对上面的新目标求对偶问题得
- 拉格朗日函数
\(L(w,b,\alpha,\xi,\mu)=\frac{1}{2}||w||^2+C\sum_{i=1}^n \xi_i\)
\(-\sum_{i=1}^n\alpha_i(y_i(w^Tx_i+b)-1+\xi_i)-\sum_{i=1}^n\mu_i\xi_i\)
- 对偶问题
\(\underset{\alpha}{min}\frac{1}{2}\sum_{i,j=1}^n \alpha_i\alpha_jy_iy_j(x_i^Tx_j)-\sum_{i=1}^n\alpha_i\)
\(s.t.\ \sum_{i=1}^n \alpha_i y_i=0,0 \leq \alpha_i\leq C,i=1,...,n\)
- 求解 （1）求解得到最优 \(\alpha^*=(\alpha_1^*,\alpha_2^*,...,\alpha_n^*)^T\)
（2）计算 \(w^*=\sum_{i=1}^n\alpha_i^* y_ix_i\)
（3）选择一个数据 \(j,0<\alpha_j^*<C\)，计算 \(b^*=y_j-\sum_{i=1}^n y_i\alpha_i^*(x_i^Tx_j)\)
（4）得到决策函数 \(f(x)=sign({w^*}^Tx+b)\)
软间隔支持向量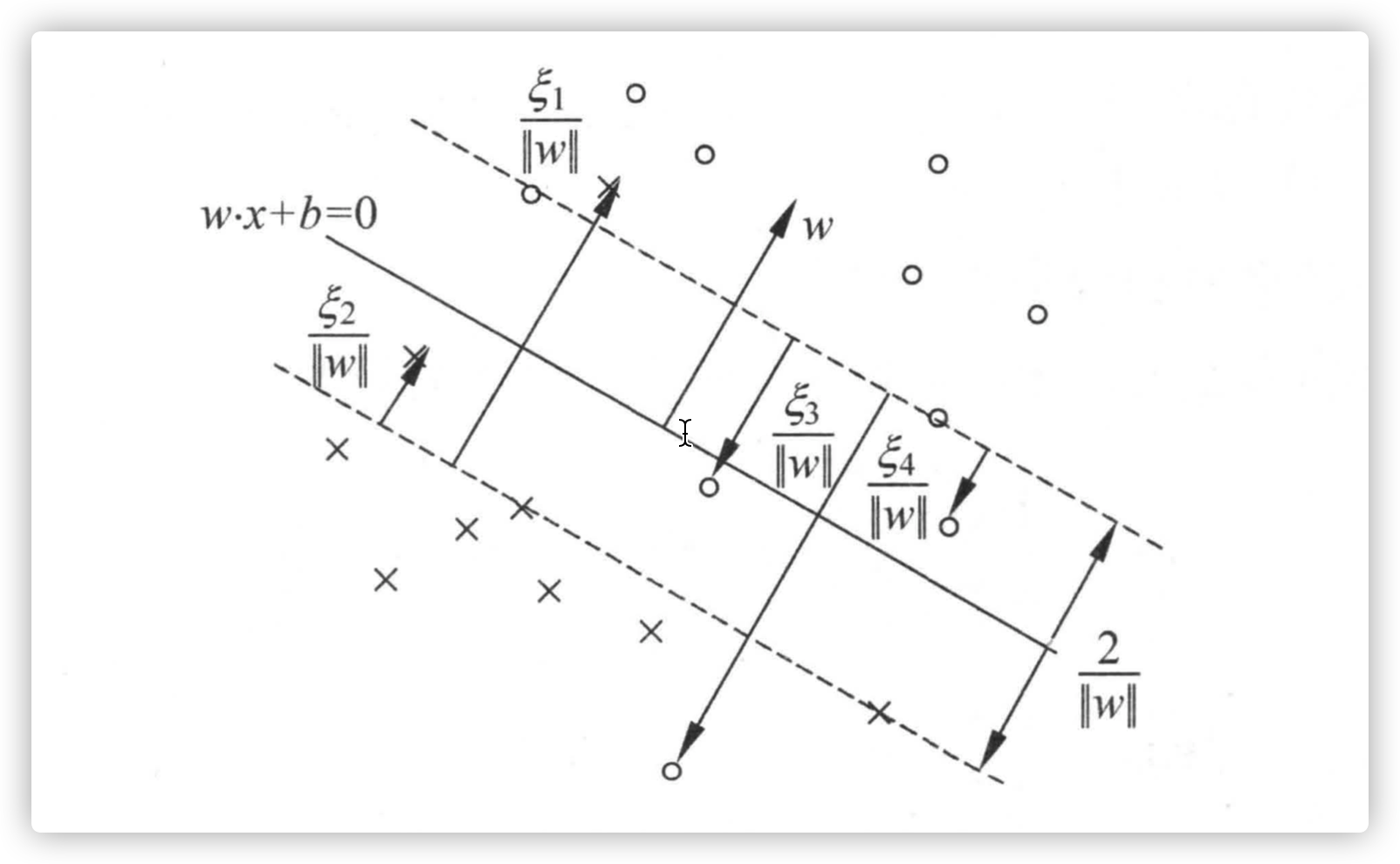 
软间隔支持向量可以在三个位置（1）间隔边界上；（2）间隔边界与分离超平面之间；（3）分离超平面误分的那一侧。 若 \(a_i^*<C\)，则 \(\xi_i=0\)，支持向量 \(x_i\) 恰好落在间隔边界上；若 \(a_i^*=C, 0<\xi_i<1\)，则分类正确，\(x_i\) 在间隔边界与分离超平面之间；若 \(a_i^*=C,\xi_i=1\)，则 \(x_i\) 在分离超平面上；若 \(a_i^*=C,\xi_i > 1\)，则 \(x_i\) 位于分离超平面误分一侧
核函数
之前讲到对原问题求偶问题，第二优点就是方便引入核函数。核函数的作用主要是为了解决线性不可分的数据。它的思想是通过隐式地将低维空间的数据隐式到高维空间，然后对数据进行线性分割，但是只需要通过低维非线性计算既可以实现。
引入核函数后的目标函数
\(\underset{\alpha}{min}\frac{1}{2}\sum_{i,j=1}^n \alpha_i\alpha_jy_iy_j\kappa(x_i^,x_j)-\sum_{i=1}^n\alpha_i\) \(s.t.\ \sum_{i=1}^n \alpha_i y_i=0,0 \leq \alpha_i\leq C,i=1,...,n\)
SMO (Sequential Minimal Optimization) 算法
SVM 推导过程：分类函数，最大化分类间隔，max1/||w||，min1/2||w||^2，凸二次规划，拉格朗日函数，转化为对偶问题，SMO算法，都为寻找一个最优解，一个最优分类平面
参考 (References)
- 支持向量机通俗导论
- 李航老师统计机器学习第2版