空间几何基础

点到平面距离公式

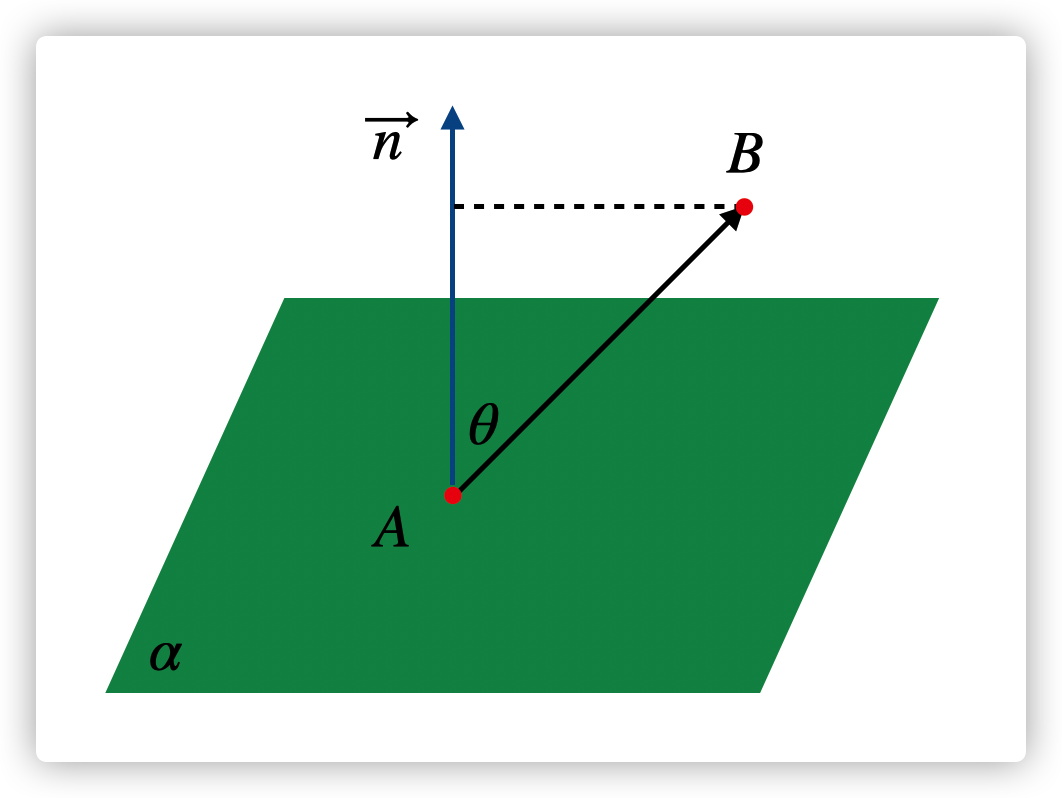
如图，有一个平面 $: \(ax+by+cz+d=0\)，它的法向量 \(\vec n=(a,b,c)\)（平面内任意一个向量与 \(\vec n\) 的点积为 0），求平面外一点 \(B=(x_1,y_1,z_1)\) 到平面 \(\alpha\) 的距离

单个高维高斯分布

\(d\) 维的高斯分布的密度函数为

\(N(x;\mu,\Sigma)=\frac{1}{\sqrt{(2\pi)^{d}det(\Sigma)}}exp\left[-\frac{1}{2}(x-\mu)^T \Sigma^{-1}(x-\mu) \right]]\)

其中 \(x\) 是一个 \(d\) 维的数据，\(\mu\) 是一个 \(d\) 维的向量，\(\Sigma\) 是一个 \(d\times d\) 的协方差矩阵

EM 基本思想

已知观察数据，未知隐含数据和模型参数。在E步，我们所做的事情是固定模型参数的值，优化隐含数据的分布（猜想隐变量的数据），而在M步，我们所做的事情是固定隐含数据分布，优化模型参数的值（基于观测数据和猜测的隐变量数据最大化对数似然函数）